Логарифм
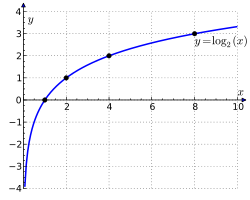
Логарифм диэн чыыһыланы хаһыс степеҥҥэ үрдэтэн бэриллибит чыыһыланы ылыахха сөбүн көрдөрөөччү. Ол эбэтэр тэннэһэр маннык суоттааһыҥҥа .Холобур: , тоҕо диэтэргин .
Логарифм суоттааһына логарифми́рование диэн ааттанар. Чыыһылалр уксугэр вещественнэй буолаллар, ол кынан баран оссо комплекснай логарифмнар теориялар эмиэ баар.
Логарифмнар туспа ураты свойстволаахтар, ол быһаарыыта олус киэҥник ыарахан суоттааһыннары чэпчэтэргэ туттуллар. Логарифмнар "эйгэлэригэр" киирдэххэ төгул олус чэпчэки эбиигэ, түҥэтии - көҕүрэтиигэ, онтон степэҥҥэ киллэрии уонна кореньтан таһаары - степэҥҥэ төгүлгэ уонна түҥэтиигэ уларыйар. Лаплас этэн турардаах, логарифм айааһына, "астроном үлэтин кыччатан, олоҕун икки төгүл уһатта". (Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь»).
Логарифмнар быһаарыыларын уонна таблицаларын суолтатын аан маҥнай 1614 сыллаахха шотландия математига Джон Непер таһаарбыт. Логарифмнар таблицалара атын математиктарынан кэҥэтэн туочунайдаан, тэҥҥэ научнай уонна инжинернай суоттааһыннарга үс үйэ тухары туттуллубута, калькулятордар уонна компьютердар айыллыахтарыгар диэри.
Кэнники буолан баран быһаарбыттарыгар, логарифмнар функциялара атын араас уобаластарга уларыйбат эбит: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Бу функция элементаарнай чыыһылаларга киирсэр, кини показательнай функцияны кытта тэҥнээн көрдөххө төттөрү. Элбэхтик вещественнэй (двоичный), (натуральный логарифм) уонна (десятичный) основаниялаах логарифмнар туттуллаллар.
Вещественнай логарифм
[уларыт | биики-тиэкиһи уларытыы]Вещественнай логарифм чыыһылата (вещественного числа) быһаарыытынан бу уравнения суоттааһына буолар. Маннык түбэлтэ буолар кыаҕа суох, тоҕо диэтэргин буоллаҕына уравнения суоттааһына табыллыбат, онтон маннык тугэҥҥэ ханнык баҕарар чыыһыла эппиэт буолуон сөп; ити икки тугэннэргэ логарифм эппиэтэ суох буолар. Иннэ кынана мыннк эппиэккэ клэбит, отрицательнай уонна нуол кыайан буолар кыаҕа суох; өссө ити үрдүнэн показательнай (показательной функции) функция наар положительнай буолар, ол иһин кыайан отрицательнай буолбат. Оччоҕуна эппиэтпит маннык буолар: вещественнай логарифм маннык усулуобуйаларга табыллар .
Элбэхтик туттулар логарифмнар:
- Натуральнай логарифм или , основаниета: число Эйлера ();
- Десятичнай логарифм или , основаниета: чыыһыла ;
- Двоичнай логарифм или , основаниета: . Кинилэр туттуллаллар: информация теориятыгар, инфроматикаҕа, дискретнай математика разделларыгар.
Свойстволара
[уларыт | биики-тиэкиһи уларытыы]Логарифм сүрүн тэҥнэһиилэрэ
[уларыт | биики-тиэкиһи уларытыы]Логарифм быһаарыытыттан тахсар тэҥнэһи:
түмүк: икки вещественнай логарифмнар тэҥнэһиилэриттэн логарифмированнай этиллии тахсар. Өскөтүн , оччоҕо , сүрүн тождестваттан тахсар: .
Логарифмнар, биир уонна тэҥ чыыһылалаах основаниялара
[уларыт | биики-тиэкиһи уларытыы]. Бу суоттааһыннар логарифм определениятыттан тахсаллар.
Төгүл, түҥэтии, степень уонна степень логарифмнара
[уларыт | биики-тиэкиһи уларытыы]| Формула | Пример | |
|---|---|---|
| Төгул | ||
| Түҥэтии | ||
| Степень | ||
| Корень |
Өскөтүн чыыһылалар отрицательнай буолра түгэннэригэр:
Төгул логарифм формулата төһө баҕар улаатар:
Логарифм основаниятын уларытыы
[уларыт | биики-тиэкиһи уларытыы]основаниялаах логарифмы основаниялаах атын логарифмҥа уларытыахха сөп:
- основания уонна логарифмируемай выражения уларыйар:
Литература
[уларыт | биики-тиэкиһи уларытыы]Теория логарифмов
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- Шахмейстер А. Х. Логарифмы. Пособие для школьников, абитуриентов и преподавателей. — изд. 5-е. — СПб.: МЦНМО, 2016. — 288 с. — ISBN 978-5-4439-0648-5



































![{\displaystyle \log _{a}{\sqrt[{p}]{x}}={\frac {\log _{a}(x)}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece430566cd091b2e5ceaf74f52fee70f36b9f0f)







